Calculo um
noção intuitiva
de limites
Aprender limites nunca foi tão fácil.
Apresentação
Site relacionado à disciplina de “Cálculo I”, da professora Vanessa, no Centro Universitário Jorge Amado – UNIJORGE, com a participação dos estudantes:
jefferson natal
Jefferson Natal Santos de Almeida
Natalício Ferreira
Natalício Ferreira Oliveira
Tom Félix
Tom Félix Figueiredo Goes
Wesley Felipe
Wesley Felipe Santos Novais
Lariane Vilela
Lariane Vilela Umburanas Dias
Filipe Assunção
Felipe Assunção Batista
joão pedro
João Pedro Silva de Santana
Icaro Conceição
Icaro conceição Oliveira
Noção Intuitiva da Limites
Introdução
Para o estudante novato de cálculo, o conceito de limite de uma função é difícil de entender formalmente e, algumas vezes, até uma noção intuitiva é pouca clara.
Mas, vamos utilizar, não somente o método matemático, mas também a nossa intuição.
Uma definição formal de limite de uma função é a seguinte (a definição a seguir foi retirada do livro Calculus: Early Transcedentals, 8ª edição, do James Stewart):
Seja �f uma função definida em algum intervalo aberto que contém o número �a exceto, possivelmente, pelo próprio número �a.
O limite de �(�)f(x), à medida que �x se aproxima de �a, é �L se, e somente se, para cada número �>0ϵ>0 existir um número �>0δ>0 tal que:
O limite é expresso por:
Essa é a famosa definição “epsilon-delta” do limite de uma função. Caso você não tenha entendido, caro aluno de Vanessa ou um outro alguém, não se preocupe, pois pelo que vi muita gente perde noite de sonos inclusive cabelos, não é atoa que engenheiro é calvo.
Uma melhor representação de NOÇÃO INTUITIVA DE LIMITES em tabela e gráfico.
Seja a função f(x)=2x+1. Vamos dar valores a x que se aproximem de 1, pela sua direita (valores maiores que 1) e pela esquerda (valores menores que 1) e calcular o valor correspondente de y:
Os que se aproximam pela esquerda:
| x | y = 2x + 1 |
| 1,5 | 4 |
| 1,3 | 3,6 |
| 1,1 | 3,2 |
| 1,05 | 3,1 |
| 1,02 | 3,04 |
| 1,01 | 3,02 |
Os que se aproximam pela direita:
x | y = 2x + 1 |
| 0,5 | 2 |
| 0,7 | 2,4 |
| 0,9 | 2,8 |
| 0,95 | 2,9 |
| 0,98 | 2,96 |
| 0,99 | 2,98 |
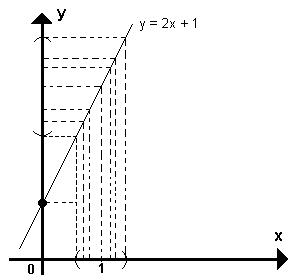
Gráfico
Notamos que à medida que x se aproxima de 1, y se aproxima de 3, ou seja, quando x tende para 1 (x 1), y tende para 3 (y 3), ou seja:
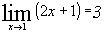
Observamos que quando x tende para 1, y tende para 3 e o limite da função é 3. Esse é o estudo do comportamento de f(x) quando x tende para 1 (x 1). Nem é preciso que x assuma o valor 1. Se f(x) tende para 3 (f(x) 3), dizemos que o limite de f(x) quando x 1 é 3, embora possam ocorrer casos em que para x = 1 o valor de f(x) não seja 3. De forma geral, escrevemos:
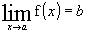
Notamos que à medida que x se aproxima de 1, y se aproxima de 3, ou seja, quando x tende para 1 (x 1), y tende para 3 (y 3). Agora ficou mais fácil de entender, não é?
Exemplos
Exemplo 01 - Aplicável
Imagine a seguinte situação: existe um menino muito arteiro, o João, que vive quebrando várias coisas em casa.
A cada travessura do Pedrinho sua mãe fica com mais raiva e ameaça: “Pedrinho! Eu estou chegando no meu LIMITE! A próxima coisa que você aprontar vai tomar umas boas chineladas”!
Mas há um problema: por mais travessuras que o Pedrinho apronte, por mais que ele quebre coisas em casa, sua mãe nunca dá umas boas chineladas nele pois seu nível de raiva nunca “chega no limite”.
Eu ilustrei essa situação da seguinte forma:
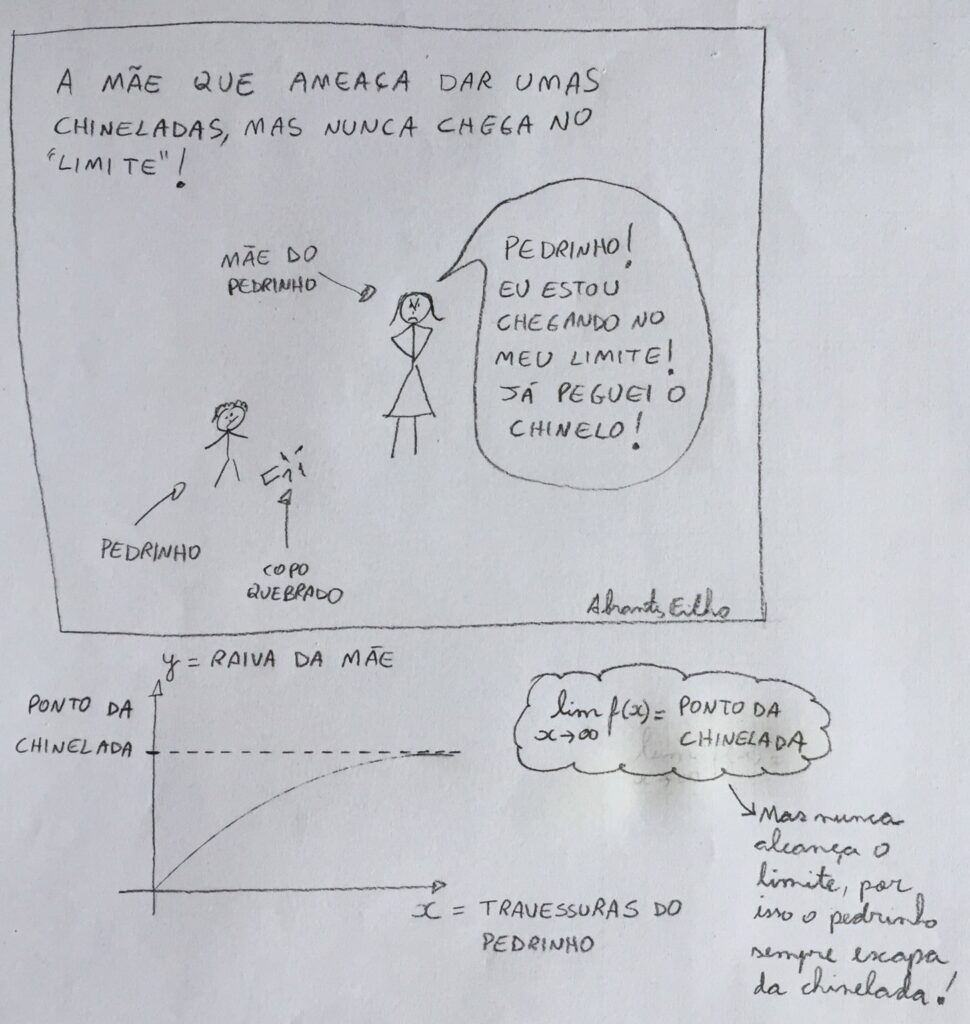
Imagem retirada do google fotos
O gráfico acima ilustra a quantidade �y de raiva da mãe como uma função �f da quantidade �x de travessuras do Pedrinho: �=�(�)y=f(x). Note que existe um nível específico de raiva da mãe que dispara as chineladas, o “Ponto da Chinelada”.
Agora repare o seguinte: à medida que as travessuras do Pedrinho aumentam, o nível de raiva da mãe também aumenta mas, na situação ilustrada, nunca chega, nunca alcança, o valor do Ponto de Chinelada, apesar de ficar mais e mais e mais próximo (assim o Pedrinho está, até agora, escapando de umas poucas e boas).
O valor do Ponto da Chinelada é o LIMITE da raiva da mãe quando as travessuras aumentam:
Ou, em linguagem mais “matemática” para a situação ilustrada:
Note que o LIMITE é o valor que a função TENDE a alcançar (a raiva da mãe TENDE a alcançar o Ponto da Chinelada) mas, não é necessário que o valor da função alcance, de fato, o valor limite.
O que importa é que, à medida que as travessuras aumentam, a raiva da mãe tende a alcançar um valor específico. Esse valor específico �L (“Ponto da Chinelada”) é o limite da função nessa situação específica (quando as travessuras do Pedrinho aumentam indefinidamente).
Exemplo 02 - Matemático
Considere a função f(x) =x1. Se olharmos para o comportamento de f(x) à medida que x se aproxima de 0, podemos observar o seguinte:
Se substituirmos valores de x próximos de zero pela esquerda, como -0.1, -0.01, -0.001, f(x) aumenta para -10, -100, -1000, respectivamente. – Se substituirmos valores de x próximos de zero pela direita, como 0.1, 0.01, 0.001, f(x) diminui para 10, 100, 1000, respectivamente. Isso indica que f(x) se torna cada vez maior em magnitude à medida que x se aproxima de zero, mas de maneiras opostas dependendo da direção. Portanto, o limite de f(x) quando x se aproxima de zero não existe.
Exemplo 03 - Matemático
Exemplo 03. Matemático – Conceito de limite em detalhes matemáticos
Considere a função g(x) = sin (x) g(x)=sin(x). Se analisarmos o comportamento de g (x) quando x se aproxima de π, podemos observar: Quando x se aproxima de π pela esquerda, g(x) diminui de 1 para 0.
Quando x se aproxima de π pela direita, g(x) aumenta de -1 para 0. Isso mostra que g(x) se aproxima de 0 à medida que x se aproxima de π em ambas as direções. Portanto, o limite de g(x) quando � x se aproxima de π é 0.